(元)支部長コラム其の11「52,53話補足:トレードを継続するための肝、資金管理を語る!」

暑の中、トレーダーの皆様はいかがお過ごしでしょうか。坂本タクマです。
今回のコラムでは、全シ連第52話、53話の補足をいたします。
52話ではシステムやポジションへの資金割り当ての話を、53話ではトレード結果のバラツキについての話をいたしました。お気づきの方もいらっしゃるでしょうが、この2話はつながっています。資金管理の1つの判断材料として、バラツキを利用できるということが言いたかったのです。
このあたりは、トレードを続けていく上での最大の肝と言っても過言ではありません。掘り下げればどこまででも深く掘れるところです。以下では、漫画には描ききれなかった話もたくさん出てきますので、どうぞお楽しみください。
システム作りと資金配分は地続き
資金配分というのは、期待値プラスのシステムを作ることができて、さらにタイプの違ういくつかのシステムをそろえることができた後のことです。ですから、今現在最初のシステムを作っておられるような方にはちょっと遠い話に感じられるかも知れません。しかし、これはシステム作りとも地続きのお話しです。システムを実戦投入するかどうかの判断基準の延長線上に、資金割り当ての基準があるからです。
漫画の中でもさらりと触れていますが、私が心がけている資金管理の大原則は、
1.いいシステムには多めに、そうでもないシステムには少なめに資金を割り当てる。
2.ひとつひとつのポジションが大きくなりすぎない。
ということです
このうちの「1」にさらに付け加えるならば、「悪いシステムには資金を割り当てない」、すなわち採用しないということです。たとえ悪くなくても、ほかにもっと使いたいものがあれば採用を見送ることもあるでしょう。いいものから順に資金を割り当てていき、割り当てるべき資金がなくなったところで、残ったシステムの採用を見送る、という考え方をすれば、同じ物差しでシステムの採用・不採用の判断と資金割り当てができるわけです。
さて、それでは「いいシステム」とはどういうものでしょうか。評価基準としては、
期待値
標準偏差(バラツキ)
ドローダウン
トレード頻度
自分に合っているか
背景にある理論を信じられるか
などが考えられるでしょう。どれを重視するかは人それぞれで、決まった正解があるわけではありません。私の場合、まず見るのは期待値、標準偏差、トレード回数です。
この3つの数字は、互いに微妙な関係にあります。期待値は高いほどよく、標準偏差は低いほど、トレード回数は多いほど好ましいのですが、これらすべてがよくなることはまずありません。期待値を上げようとすれば、どうしてもトレード回数は減りがちになります。全部がよいスーパーなシステムを作るのが難しいからには、これらのバランスが取れているのがいいシステムだ、と私は考えています。
バラツキを心配する
ここで、バラツキの指標である標準偏差がひとつのカギを握ります。この、一般にはイマイチ使い方の知られていない指標の使い方は、例えばこういうことです。ある車種の自動車と、ある機種のタブレットPCの、どちらの価格がよりバラついているか、という問題があったとします。いろいろな店を調査した結果、下のようであったとします(数字は架空のものです)。
| 平均 | 標準偏差 | |
| 自動車 | 205.1万円 | 20.3万円 |
| タブレットPC | 4.2万円 | 0.58万円 |
単純に標準偏差だけを比べれば、自動車のほうがだいぶバラついているように見えます。しかし、これだけ価格帯の隔たったものを、そうやって比べていいものでしょうか?そこで考え出されたのが、「変動係数」というものです。下のような式で計算します。
変動係数 = 標準偏差 ÷ 平均
これをそれぞれについて計算してみると、
| 変動係数 | |
| 自動車 | 0.099 |
| タブレットPC | 0.138 |
となり、タブレットPCのほうがややバラついている、と言えそうです。
シストレ関連の本にときどき現れるのは、この変動係数の逆数、
期待値(利益率の平均) ÷ 利益率の標準偏差
です(これの正式名称がいまだに分からないのですが)。逆数を取ることによって、「大きい方がよい」というふうに、トレーダーにとってわかりやすいものになっています。変動係数のままだと、「小さい方がよい」となるのですが、そうすると期待値マイナスの場合に矛盾が生じます。
この値を上げたければ、期待値を高くし、標準偏差を低くすることです。両方成し遂げるのが難しければ、どちらか一方だけでもよくして、改善を試みます。期待値が大きければ、バラツキのことはあまり気にする必要はないでしょう。期待値がギリギリプラス、みたいなときには、バラツキには神経質にならざるをえません。
漫画には、「ヤバいのはマイナス方向のバラツキなのだから、そっちだけケアすればいいのでは?」という質問が出てきました。投信などの評価に使われるシャープレシオ(分母が標準偏差)の改良版として、ソルティノレシオ(分母が下方偏差)というのが出てきたことからも、そういう考え方をする方は多いと推察できます。
私の結論としては、「どっちでもいい」ということです。下のほうのバラツキを小さくしようとすると、上の方のバラツキも小さくなりがちだ、と経験上感じています。もしマイナスのほうのバラツキだけキュッと小さくして、プラスのほうのバラツキは大きいままにできたとすれば、期待値がガツンと上がるはずです。いずれにせよ、期待値÷標準偏差の値はよくなるのです。というわけで、「全体の標準偏差」を使おうが、「マイナストレードの標準偏差」を使おうが、結論はそう変わらない、少なくとも致命的な差は出ない、というのが私の考えです。
ただし、プラス方向のバラツキを考慮しないと、1つ心配なことがあります。特にシミュレーション上の総トレード数が少ないときに、本来の性能以上の結果が出かねない、ということです。
これは、このコラムの第9回でも述べたことです(其の9、実験2-6参照)。本来の性能では期待値がわずかにマイナスで、バラツキの非常に大きいシステムがあったとき、少ないトレード数ならば、結構な頻度で右肩上がりに見えてしまうことがあるのです。
しかしこれについては、「システムの本来の性能って何?」というような難しい問題もあり、この議論であっているのかどうか今ひとつ自信が持てません。今のところは、自分は一応こういう点にも用心している、と述べるに留めておきます。
割当金額の増減法・マニアックバージョン
こうして、期待値や標準偏差やトレード数に自分の心理面のあれこれを加味してシステムの良し悪しを判断したならば、いよいよ資金割り当てを考えます。方程式を解いて唯一絶対の最適解を求める、というような難しい話ではありません。自分が投資に何を求めるのか、各システムにどれくらい期待するのか、という気持ちを表す表現行動、それがマネーマネジメントだと思っています。
素朴なやり方としては、総資産の m% をシステムAに、n% をシステムBに・・・というふうに分ける方法があります。また、「初期割当金額+そのシステムで稼いだ利益」をそのシステムの割当金額にするという方法もあります。これは、システムごとに口座を分けることで簡単に実現できます。
もちろん、こういった方法で普通は十分です。このようなやり方で儲けている方もたくさんいらっしゃいます。
私の場合は少々マニアックでありまして、システムごとに割当金額の増減法や仕掛け株数の決め方を変えております。
下の表をご覧ください。漫画にも出てきましたが、もう一度掲載致します。
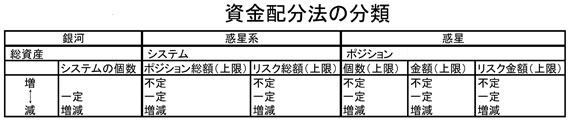
システムごとにこの表を埋める形で、資金管理ルールを作っていきます。このシステムは自信があるので総資産に比例させて割当金額を増やそう、とか、これはそうでもないんで係数の小さな1次関数で緩やかに増やしていこうとか。
「比例」と「1次関数」という言葉を使いましたが、「中学数学ヤバい」という方のために念のためご説明いたしましょう。
式で表せば、比例とは
y = ax
1次関数とは
y = ax + b
という形です。xに総資産額などを入れれば、yとしてそのシステムやポジションへの割当金額が出てくる、という仕組みです。
比例も1次関数の一種ではありますが、いわゆる「切片」がありません。上の式でいえば「b」にあたる部分です。割当金額を「比例」で決めたら上下動は激し目になり、「1次関数」で決めたら緩やかにすることができます。
例を見ていただきましょう。初期の総資産が1000万円、あるシステムへの初期割当金額を400万円とします。この割当金額を、「比例」で増やしていく場合と「1次関数」で増やしていく場合で、どのような違いが生じるか見てみましょう。「比例」の式は y = 0.4x、「1次関数」の式は y = 0.1x + 3000000 とします。
| 総資産 | 1000万 | 1500万 | 1500万 |
| 比例 | 400万 | 600万 | 800万 |
| 1次関数 | 400万 | 450万 | 500万 |
比例のほうは資産の増加がダイレクトに反映されますが、1次関数のほうはそれよりはゆっくり目です。y = ax + b のaとbをいろいろ変えることで、スピードを調節できます。もちろん、aの値は0と1の間で、しかもけっこう0寄りにしておくのが御身のためでございましょう。
1次関数の代わりに、平方根を取ったり、対数を取ったり、いろいろな関数を使うことでいろいろスピード調整ができそうですが、ここではこれ以上話を難しくするのはやめておきます。2次関数みたいに、どんどん上がり方が急になっていくようなのは使わないほうがいいんじゃないか、ということだけは申上げておきます。
xに何を入れるか、というのもいろいろ考えどころの多い問題です。システムへの割り当てに関してなら、総資産とか、そのシステムでの儲け金額などを入れることが多いでしょうか。システム内の個々のポジション金額ならば、そのシステムへの割当金額に関する1次関数とか比例を使うことが多そうです。
幅が広いのは、ポジションのリスクをどう捕えるか、というところです。ざっと挙げれば、
・仕掛値と損切値の幅(最大許容損失)
・直近のボラティリティー(ATRなど)
・仕掛値とチャート上の n日高値・安値までの幅
・過去データ上の最大損失
・過去データ上の下位 m% に相当する損失
・過去データ上の平均損失
まだまだあるでしょうが、こういったものに基づいてポジションのリスク金額の上限を決めるわけですけれども、その際にも総資産やシステムへの割当金額に比例させるのか、1次関数でいくのか、それとも資産額に関係なく一定にしておくのか、と様々で、もう尋常じゃない組み合わせが存在します。
一例を挙げれば、
最大許容損失 ≧ 0.02 × システムに対する割当金額
を満たすように仕掛け株数を決める、というふうにするわけです。
ポジション金額の上限だけ決めておいてリスクは決めないとか、その逆とか、システムへの割当金額さえ超えなければポジションごとの金額やリスクには制限をかけないとか、いろんなやり方が考えられます。
私の場合は、自信があって多めに資金を割り当てているシステムでも。原則の「2」に挙げた「ひとつひとつのポジションが大きくなりすぎない」を守るために、ポジション金額もリスク金額も1次関数でゆっくり増えるようにしています。
いろいろ言ってきましたが、要するに大変な自由度なのです。漫画では宇宙に例えましたが、なにか絵を描くことにも似ていると思えてきました。構図を決めるところから始まって、大ざっぱに描いていってから細かいところを描き入れる、みたいな。まさにマネーマネジメントは表現活動です。
何を選択するかは、投資の目的次第です。半年で10倍にする、というなら破産覚悟でリスクを相当大きく取らなければならないでしょうし、とにかく穏やかに、夜はぐっすり眠りたいというのであれば、すべてを小さめの額で「一定」にすることもできます。こればっかりはその人の価値観に属することなので、他人がとやかく言うべきものではありません。
ただし、どんなに優秀な売買ルールをお持ちでも、かなりの確率で破産するような大きなリスクを取れば、やはりかなりの確率で破産するものです(其の9、実験2-2参照)。表現の自由も数学的真理には逆らえない、といったところでしょうか。
おわりに
いかがでしたか。何か使えるアイデアはあったでしょうか。肝心の部分がぼんやりしている、とお感じになったかも知れません。それは致し方ないことです。トレーダー各位のお考えにゆだねられている部分も大きいのです。
どのような資金管理法を使うにせよ、適宜見直しをすることが必要でしょう。なるべく自分の目標に合うように、あるいは目標の変更に合わせて、常に改善することです。画家が油絵に何年にもわたって手を入れ続けるように、マネーマネジメントに向き合い続けるのです。
私自身、これからもずっと改良し続けていくでしょう。そのたびに、自分でこの文章を読み返すことでしょう。そしてこの文章自体に改善すべき点が見つかったら、この場で皆様にご披露することでしょう。その過程で、また新たに自分の資金管理法の改善点が発見されて・・・
すべてはぐるぐると回っていくのです!宇宙のように!!